An Introduction of Union-Find Disjoint Sets

City Connections

Let us consider a scenario of building cities with roads. A map of city can be regarded as a bunch of junctions of roads, the question is how we can figure out if I can get from a junction to another junction in a efficient time. To solve this problem, we can adopt Union-find Disjoint Sets (or disjoint sets).

Reading in Roads Info

Since we are curious about how the roads in the map are connected. Let we mock up some data, let say:

1 -- 3
1 -- 2
2 -- 4
3 -- 4
5 -- 6
6 -- 7

The notations -- indicate a interconnection of each pair of junctions. We can build a graph according to the specification, like this:

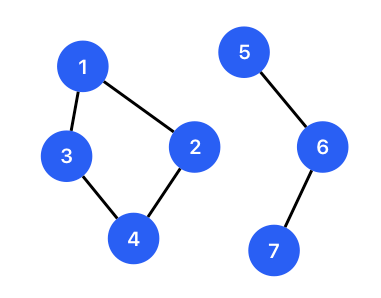
In this graph, if we want to check if node 4 is connected with node 7, we can use search algorithms such as Depth-first Search (DFS) or Breadth-first Search (BFS). If we want to make sure we cannot go to node 7 from node 4, we must traverse all around the left 1-2-4-3-1 graph. The time complexity of checking is O(N).

If we just want to know if they are interconnected, the more time-saving way is to build disjoint sets, then we can lower down the time complexity with the help of trees.

How it works

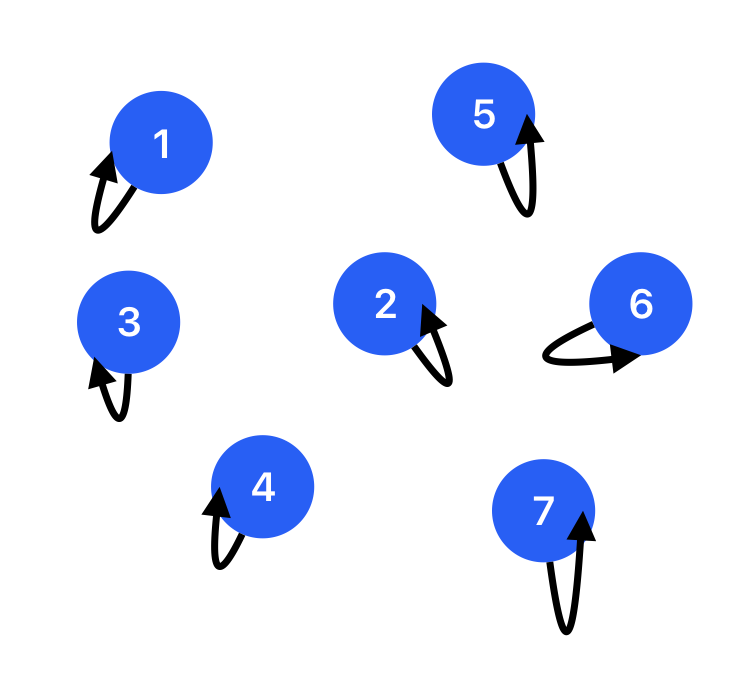
To model this problem, we can regard each traffice junctions as a node, as shown in the figure. At first, we can initiate each node having their parent node as itself since disjoint sets work with tree data structures (tree have a root node). In the current scenario, every node is a root node and there are 7 trees in this figure, which can easily illustrated by the Python code:

parents = [0, 1, 2, 3, 4, 5, 6, 7] # index 0 omitted

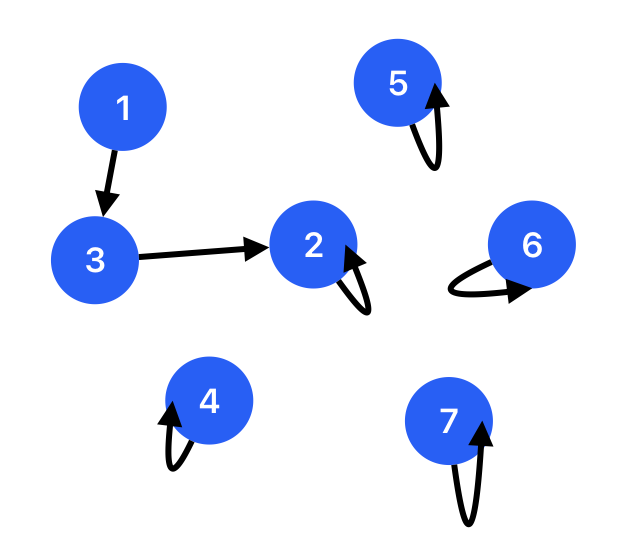
Now we read in the data of how the junctions connected. Such as 1 -- 3, we need to change the parent of one node to another (whatever it is node 1 or node 3). The diagram illustrate the result of disjoint sets after alternation.

parents = [0, 3, 2, 3, 4, 5, 6, 7]

Okay, seems easy. Let us do the next link, 1 -- 2. Follow with the rules of tree, a node in a tree can only have one parent. If we change the parent of node 1 to node 2, node 3 could no longer be parent of node 1, which causes loss of information. The solution is pretty straight-forward, since each root node have parent node as themselves. Since each group of interconnected nodes can be identified by different root nodes, if node 2 want to join the group which having root node is node 3, then just simply change the parent of node 3 (group root node) to node 2.

Here are the rules:

1. If we are going to link two nodes which are in different groups (single node is also considered as a group), link the root nodes of  each groups together.
2. If we are going to link two nodes which are in the same group (having the same group root node), do nothing.

The Python code for finding a group's root node is:

def parent_of(node):
  if parents[node] is not node:
    return parent_of(parents[node])
  else:
    return node

By applying the rule, we can finally get following trees after linked 6 -- 7:

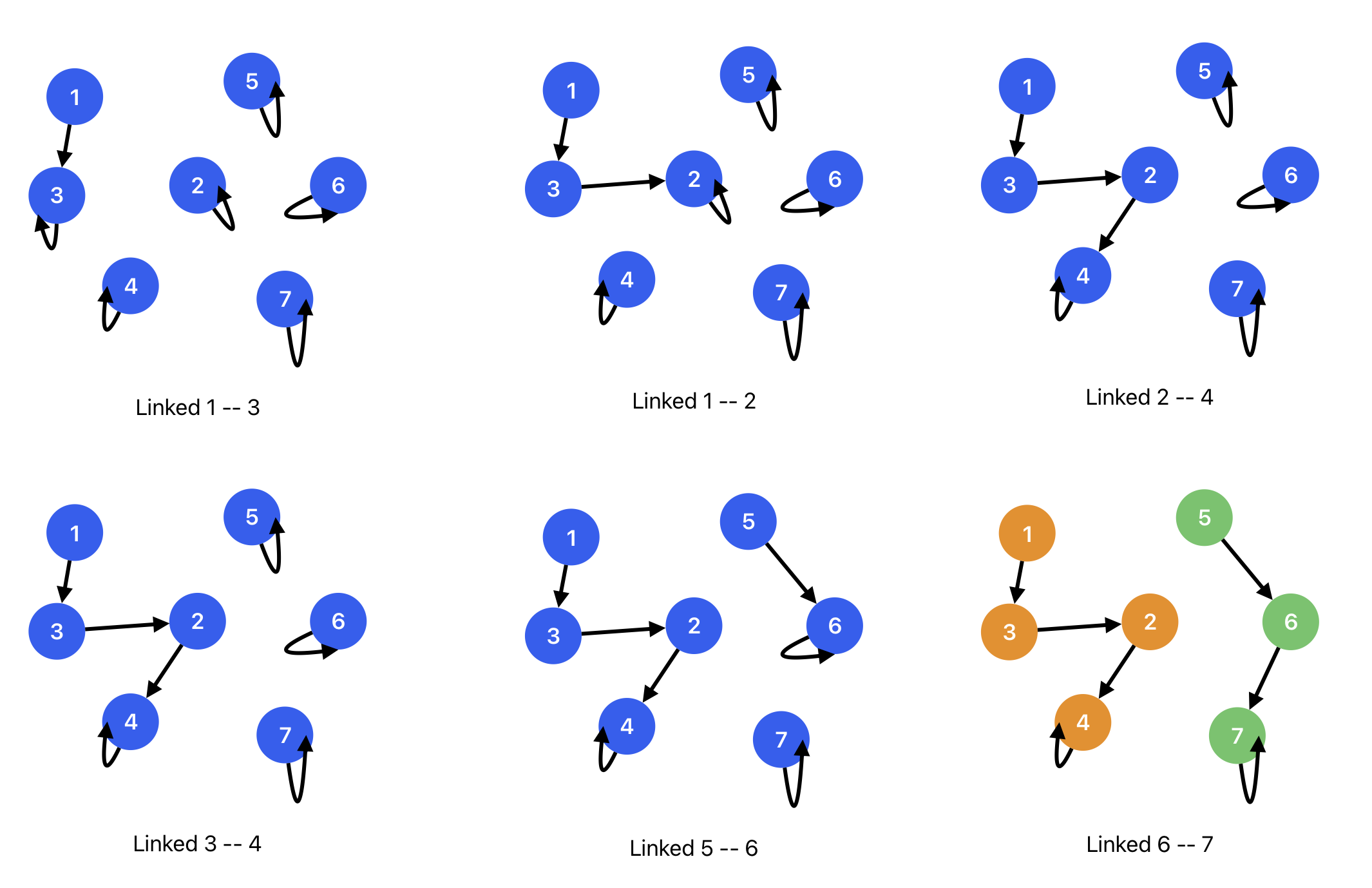
In the final result, 6 -- 7, we have two groups, root node 4 and root node 7. Back to the question, to check if node 4 and node 7 are interconnected, we need to check if parent_of(4) is equal to parent_of(7).

However, currently, the worse case of disjoint sets is that trees are builded as a linked list (degenerate into a chain), as the example given. The time complexity is still similar to that of utilizing search algorithms. To tackle the issue, we must update the current disjoint set into a 1-depth tree, as illustrated in the following figure.

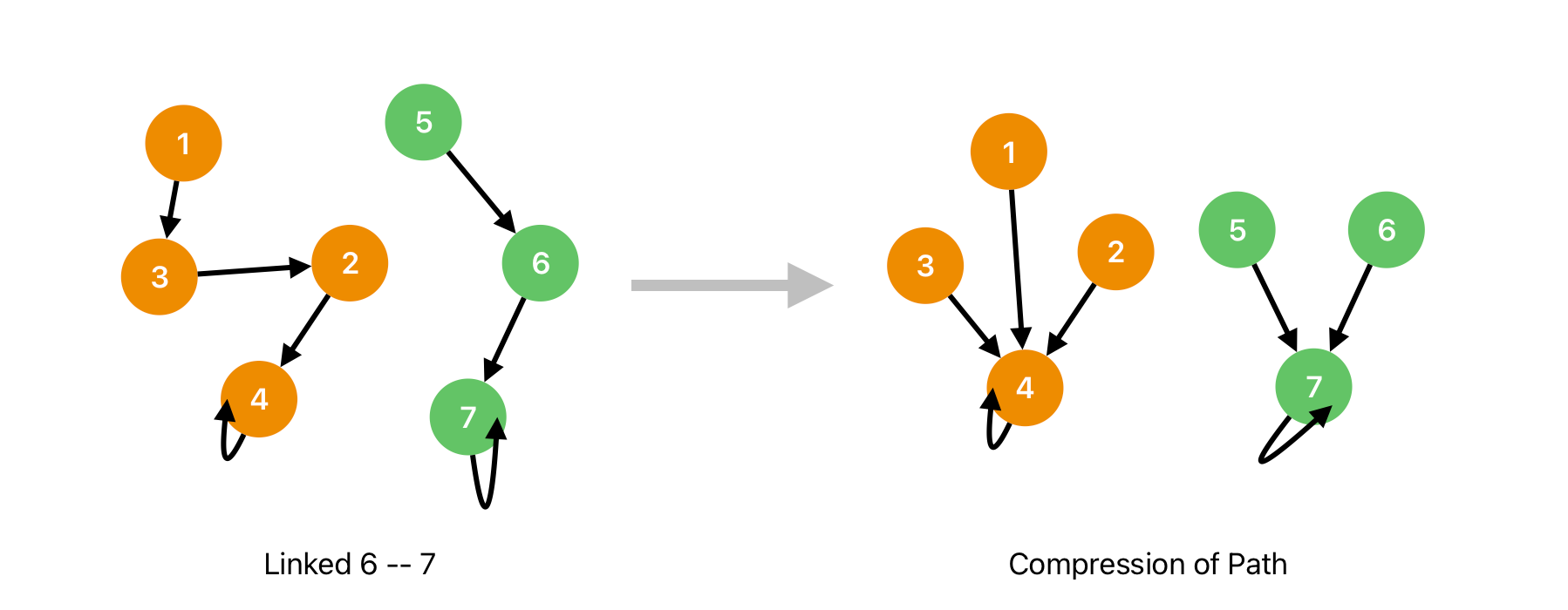
The following updated parent_of(node) function can implement this action

def parent_of(node):
  if parents[node] is not node:
    parents[node] = parent_of(parents[node]) # update parent of node to root
    return parents[node]
  else:
    return node

When we get disjoint sets after compression of path, the time complexity of checking if two nodes are interconnected will be optimized.