Aho–Corasick Automaton

The mathematical stuff

It is essential to have a knowledge of some mathematical stuff before introducing the Algorithm. And the math here is really straightforward.

Finite-state machine(FSM) is a mathematical model of computation. It can change from one state to another in response to some inputs. Here is a practical example for a quick glance at the FSM.

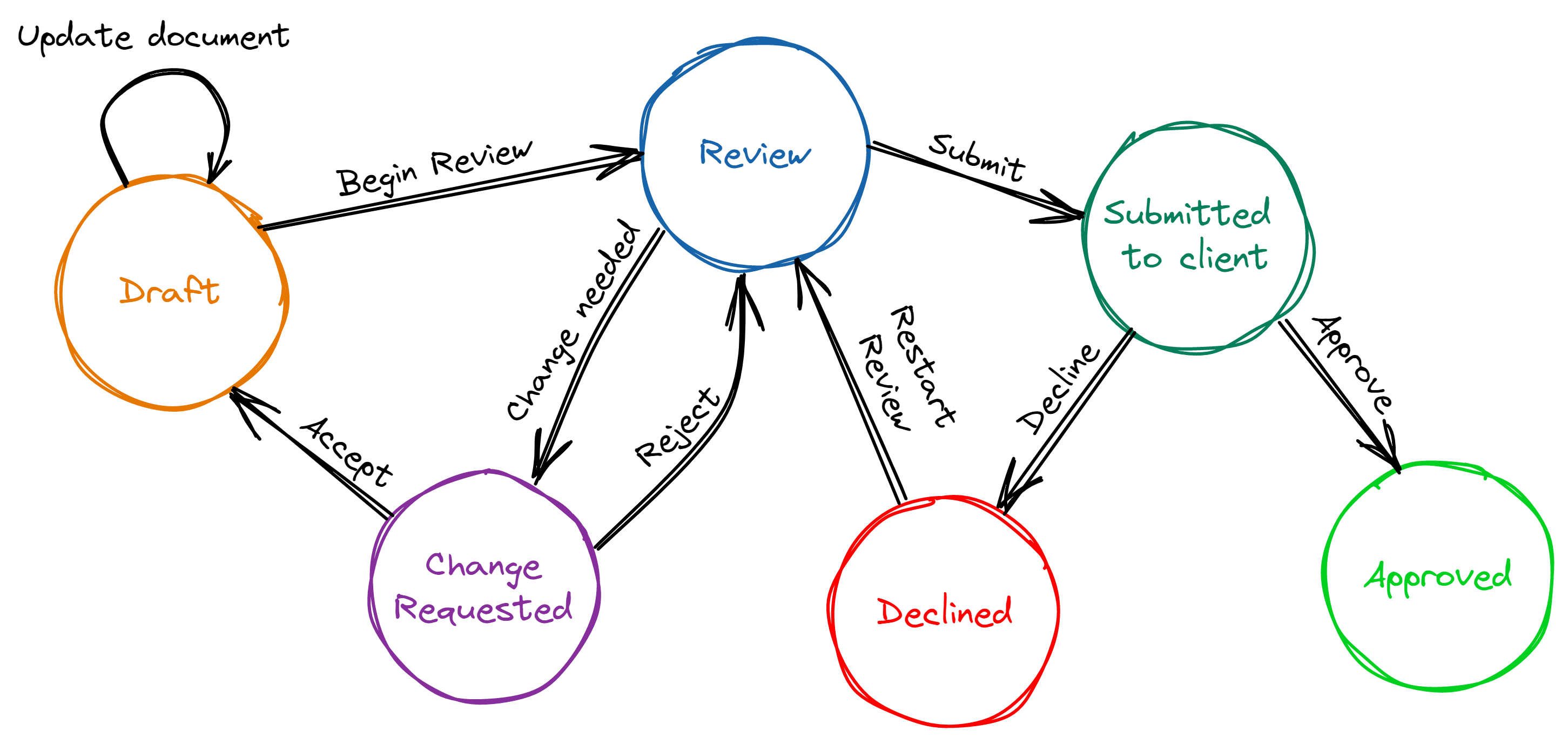
From the example you can see that the term FSM is just an abstract for a bunch of processes of the statute that can change during the inputs(like "Begin Review", "Submit", ...). For an abstract version, take a look at the following graph.

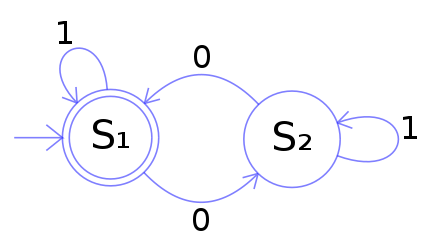
It is worth mentioning that S1 here, which has a double circle, is the starting or beginning status. And we can see that, within a bunch of inputs of 1 and 0, we can stand of either S1 or S2 and it depends on what sequence of inputs we have.

For this S1-S2 automaton, assume we have input is [1, 0, 1, 1, 0]. Then the state change is S1 → S2 → S2 → S2 → S1.

Now, the mathematical part is finished. Now the exciting part is beginning.

Trie

A trie, also called dictionary tree or prefix tree, is a tree-like data structure for finding a word(determining if the word has been added to the set). Here is an example:

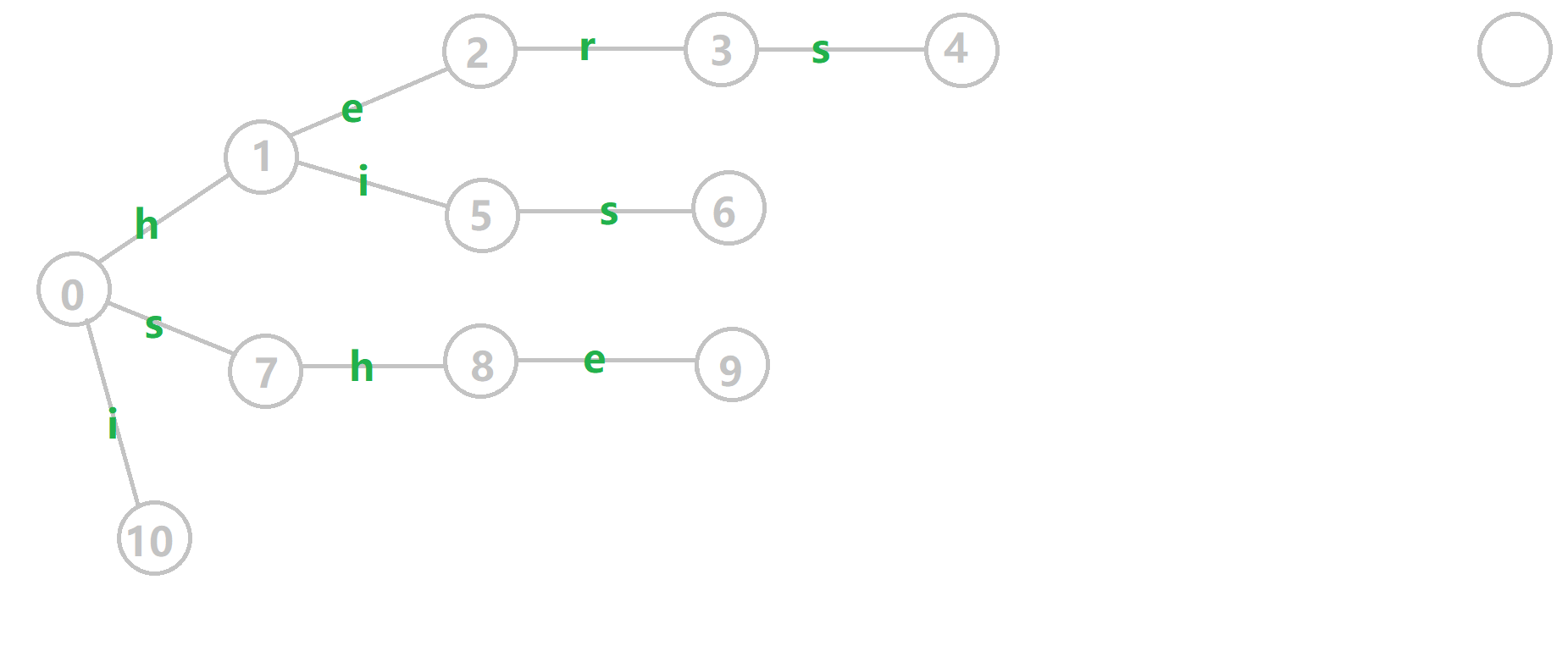
Here are the features of a Trie.

• The root node of Trie is 0
• Each character is marked on the edge
• Leave nodes(4, 6, 9, 10) must mean the ending of a word
• Other nodes(1, 7, 10, 2, 5, 8, 3) may mean the ending of a word

Which means:

• If this trie is constructed with the dictionary [hers, his, she, i], then nodes 4, 6, 9, and 10 are the ending of a word.
• If this trie is constructed with the dictionary [he, her, hers, his, hi, she, i], then nodes 2, 3, 4, 5, 6, 9, 10 are the ending of a word.

Besides, for each non-leaf node (including root), each edge that links to the child node is unique. In another word, node 0, has three edges namely h, s, i. It is illegal when having edges h, h, s, i, that is because it contains two h edges.

Aho–Corasick Automaton: Fail pointer

Aho–Corasick Automaton can be achieved due to the Trie. And this Algorithm upgrades the Trie by adding fail pointers. Fail pointers are like a Portal in certain nodes on the Trie tree. When you step on the "Portal node", it could send you to another node.

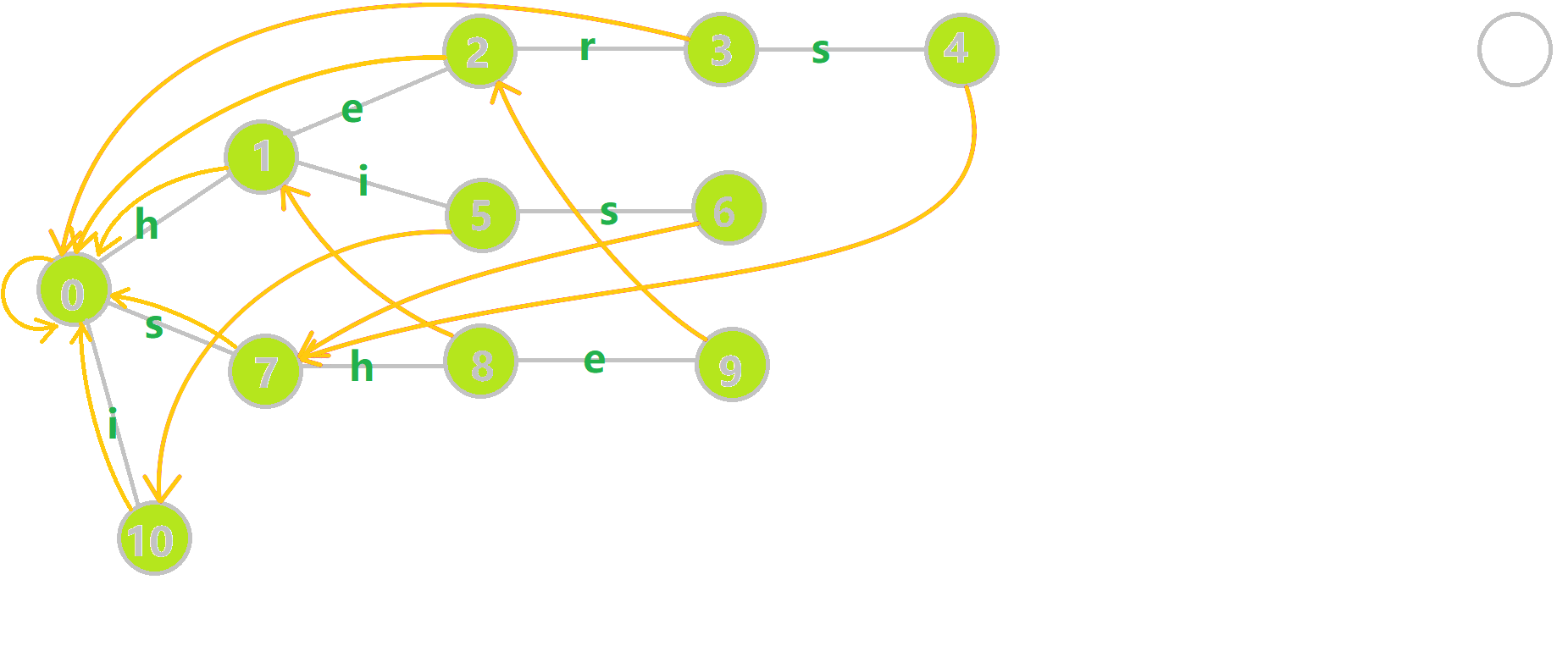
Here are the fail pointers(in yellow arrows) for the previous Trie. The fail pointers are constructed by a tiny Algorithm which I will introduce later. Now we shall play with the upgraded trie with fail pointers. We can see that:

• Each node has a fail pointer
• The fail pointer of a node is either point to root node or point to another node

Now is the Algorithm for the construction of the fail pointer:

Consider a trie with the current node u, the parent node of u is p, p go through the edge of the character c(s, h, e, ... in this example) to u. That is represented by trie[p, c] = u. Assume that all the fail pointers whose depth is smaller than the depth of u is determined:

1. If trie[fail[p], c] exists: let fail[u] be trie[fail[p], c]. This means adding character c after p and fail[p] and corresponding to u and fail[u]
2. If trie[fail[p], c] not exists: find trie[fail[fail[p]], c] recursively and go back to step 1. Until fail pointer points to the root node.
3. If the fail pointer points to the root node: record fail[u] = root

The code for constructing fail pointers is shown in Python:

def build():
    for i in range(0, 26):
        if tr[0][i] == 1:
            q.append(tr[0][i])
    while len(q) > 0:
        u = q[0]
        q.pop()
        for i in range(0, 26):
            if tr[u][i] == 1:
                fail[tr[u][i]] = tr[fail[u]][i]
                q.append(tr[u][i])
            else:
                tr[u][i] = tr[fail[u]][i]

Aho–Corasick Automaton: Matching

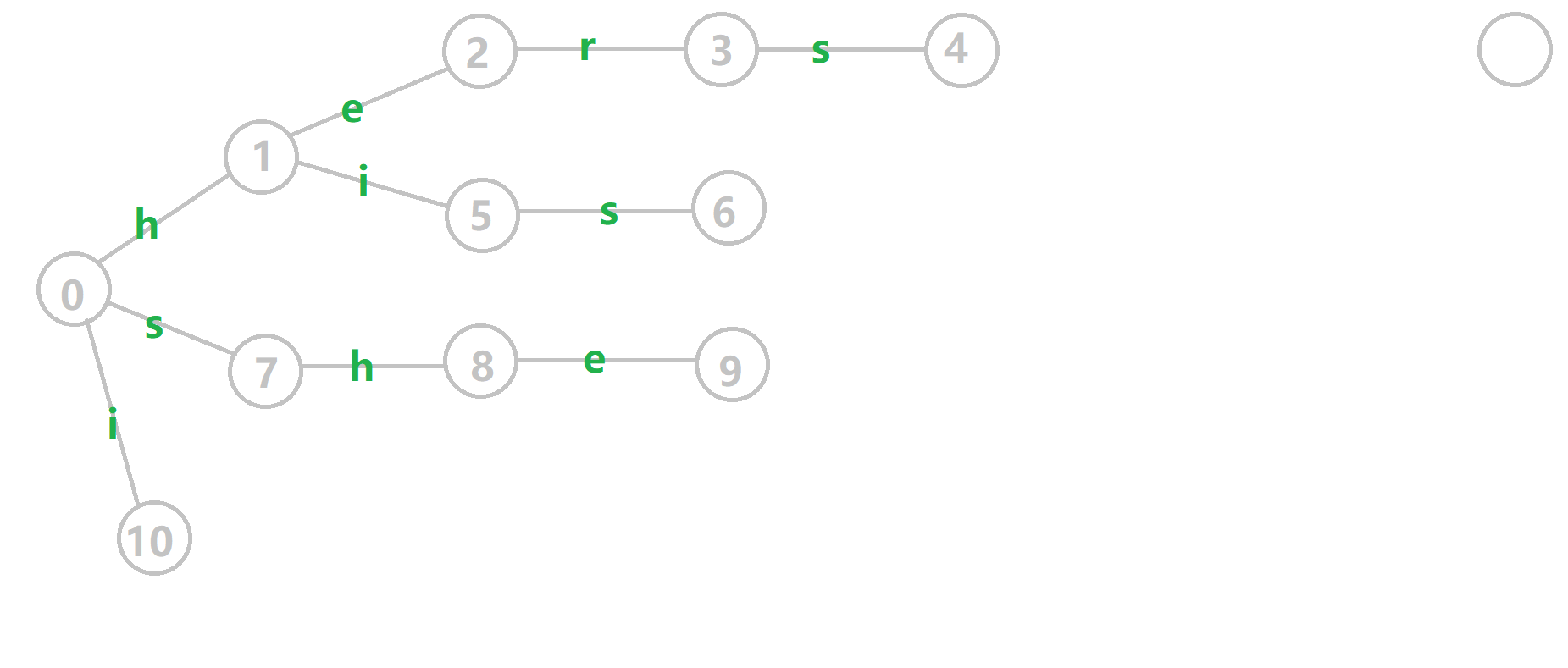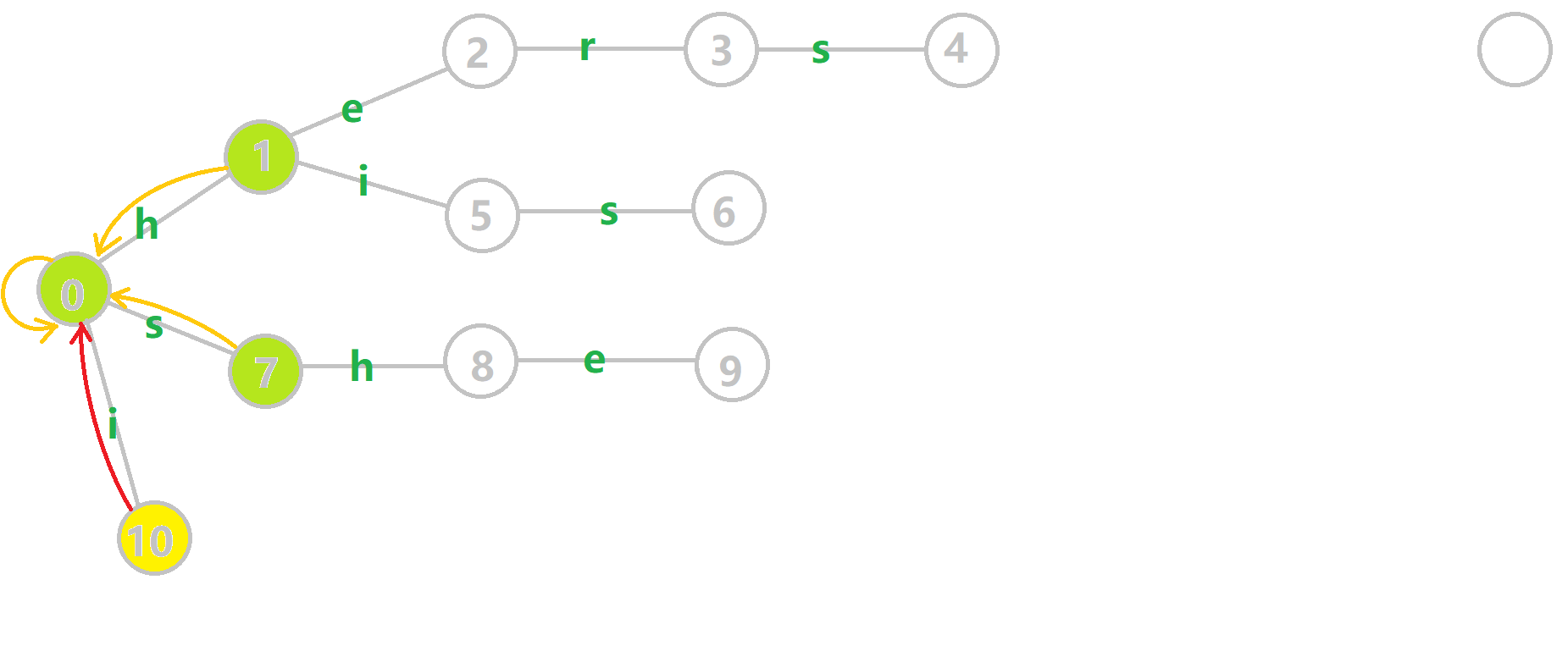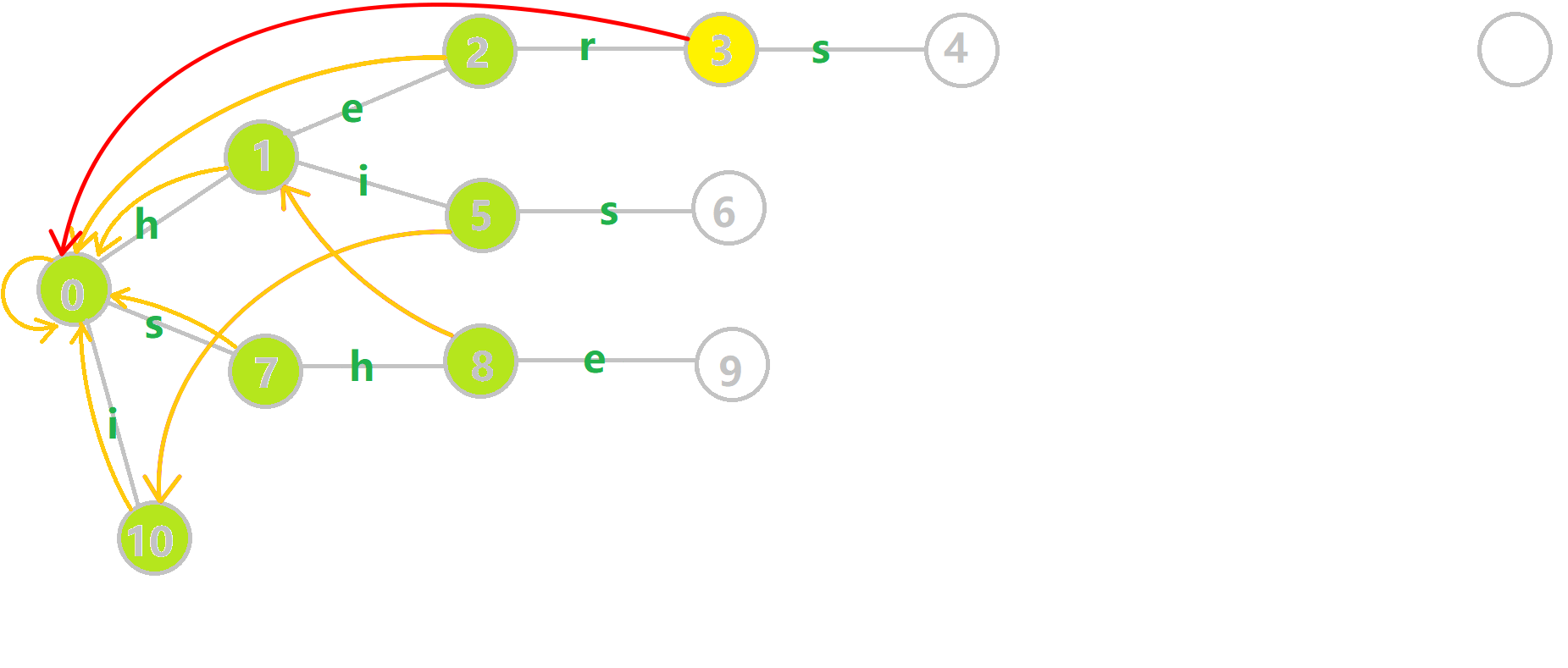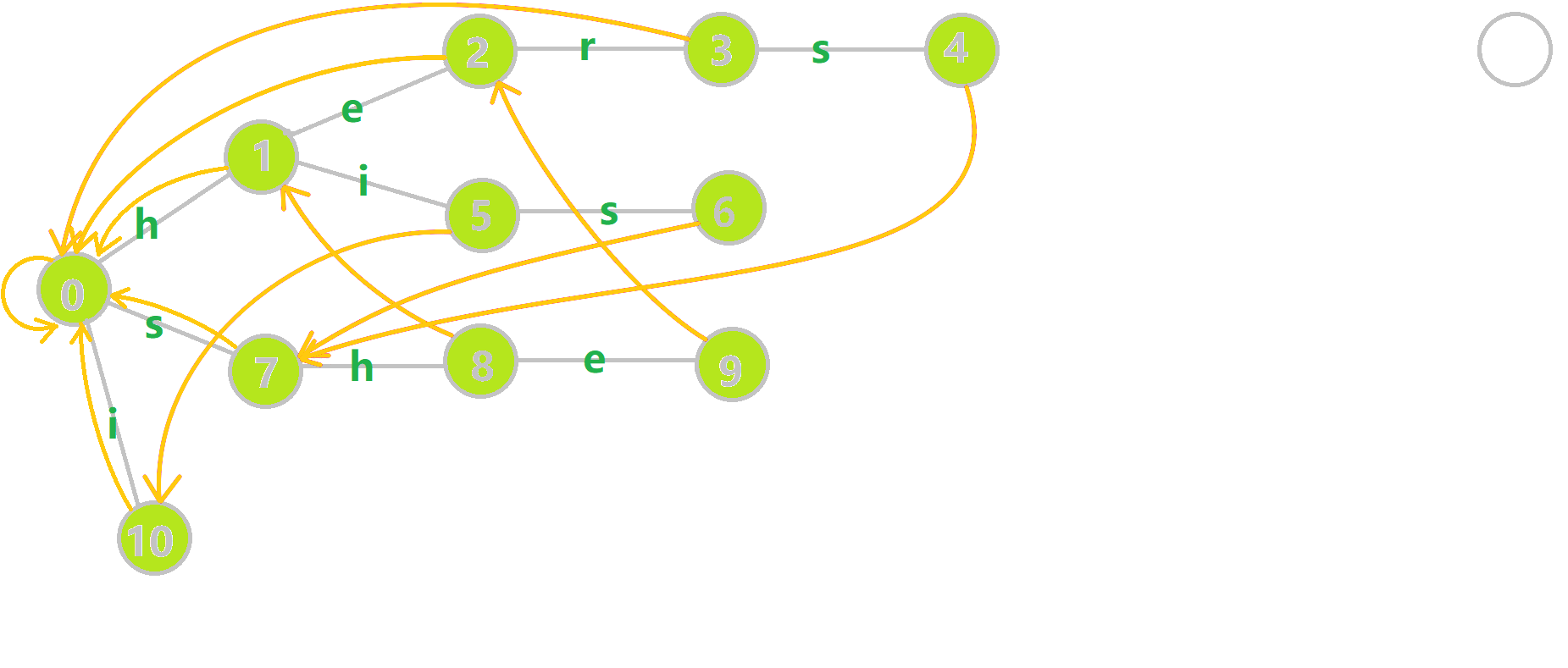
Here as the currently matched node on the dictionary tree, res is the returned answer. Loop through the matching string, keeping track of the current character in the dictionary tree. Use the fail pointer to find all matching patterns and add them to the answer. Then clear. As we have analyzed above, the structure of the dictionary tree is actually a trans function, and after constructing this function, in the process of matching strings, we will discard some prefixes to achieve the minimum matching. The fail pointer points to more matching states.

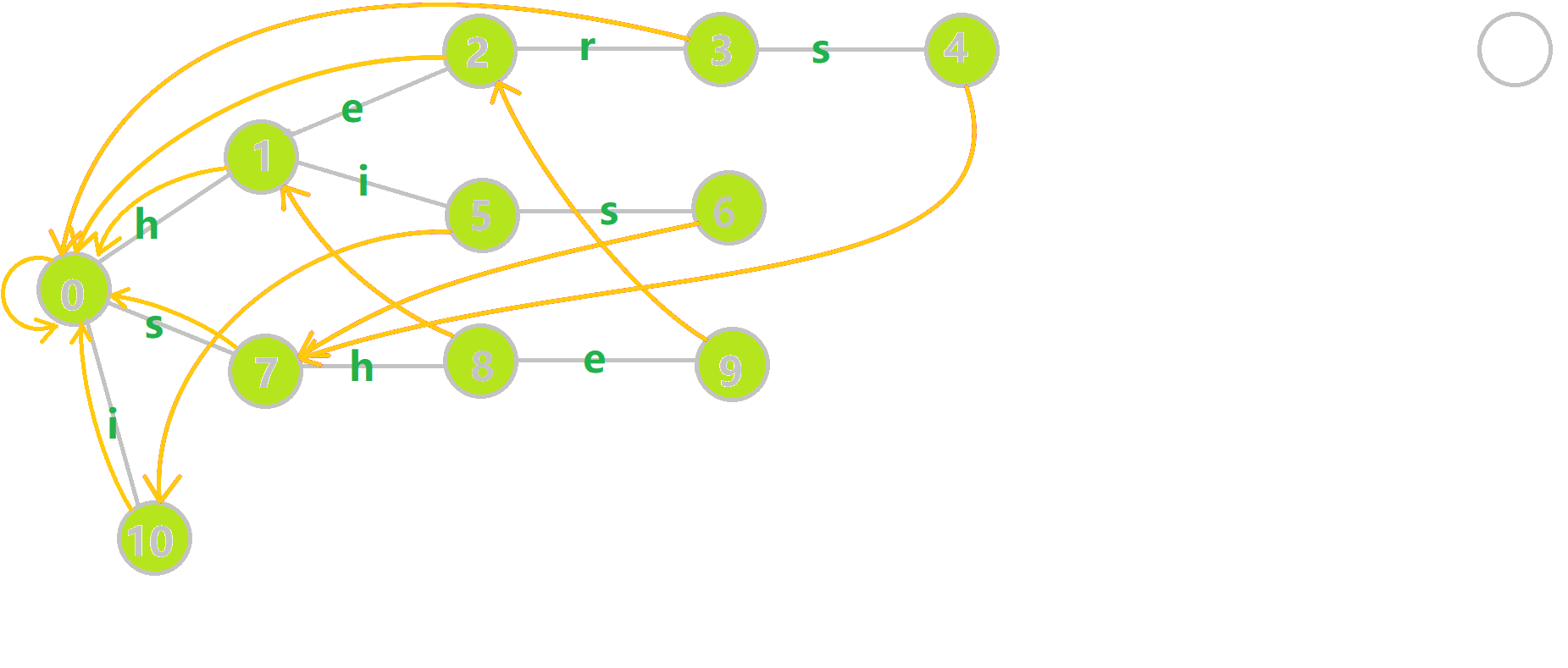
If we match a document ushersheishis, The status trans will be:

(0) - s → (7) - h → (8) - e → (9: she) → (2: he) - r → 
(3: her) -s→ (4: hers) → (7) -h→ (8) -e→ (9: she) → 
(2: no edge i, back to root) → (0) -i→ (10: i) → 
(0) -s→ (7) -h→ (8) → (1) -i→ (5: hi) -s→ (s: his) → EOF

And we find words with frequency:

she: 2
he: 1
her: 1
hers: 1
i: 1
hi: 1
his: 1

Time complexity

Preprocessing stage Θ(n):

• Θ(n) work to build the trie,

• Θ(n) work to fill in suffix links,

• Θ(n) work to fill in output links.

Final Totals ⟨O(n), O(m + z)⟩:

Reference

https://web.stanford.edu/class/archive/cs/cs166/cs166.1166/lectures/02/Small02.pdf

https://oi-wiki.org/string/ac-automaton/