An Introduction to Monotonic Stack

A Monotonic Stack is a stack where elements are maintained in a specific order: ascending, descending, or based on user-defined properties. This structure saves time on comparisons and improves algorithm efficiency.

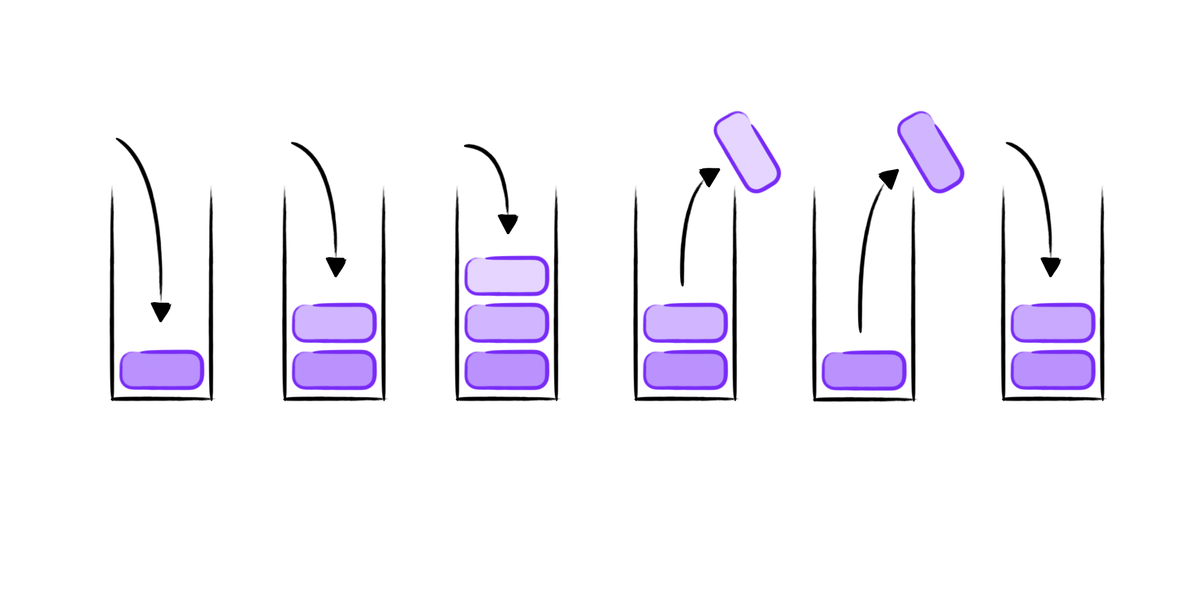
A Monotonic Stack, as its name suggests, is a stack where all elements are maintained in a specific order: either ascending, descending, or based on user-defined comparable properties. The characteristic of this data structure is the maintenance of this order, which can save time on certain types of comparisons and improve the efficiency of some algorithms.

An Example

Given an array to be pushed into a monotonic descending stack, say this array is [5, 3, 1, 7, 6, 2]. The first three elements pushed into the stack are:

[buttom -> top
[5
[5 3
[5 3 1

And for the next one, 7, which is greater than the top of the stack (1), the stack will be popped until it meets one of the following conditions:

Stack is empty
Stack top is greater than the next element (7)

So the stack will iteratively be:

[5 3 1
[5 3
[5
[
[7

And then 6 is smaller than the top of the stack, so push it. So do the final element 2.

[7 6
[7 6 2

The property of this data structure is that the top of the stack must be the extremum value (either maximum or minimum)

Solving Problems

Here are some problems that you can solve using a monotonic stack. I will explain one of them, the Bad Hair Day. The second one, Trapping Rain Water, is an exercise for you.

POJ 3250 Bad Hair Day

One of the examples is "Bad Hair Day" from USACO 2006 November Silver (this link will redirect you to POJ.org).

POJ 3250 Bad Hair Day Description

$N$ cows standing from left to right, $h_i$ is the height of cow $i$. $c_i$ is the number of cows between cow $i$ and the first cow standing on the right of and taller than cow $i$. Determine the value of $\sum\limits_{i=1}^{N} c_i$.

To solve this problem, we can use a monotonic descending stack, accumulating the answer each time the stack pops. Say we have height = [10, 3, 7, 4, 12, 2] represents the height of each cow. After push two indices (not element) into the stack,

[0
[0 1

we meet a cow 3 (height of 7) which is greater than the top of stack, which means, the stack top cow 1 (height of 3) can see 0 (index of cow in height of 7 - index of the stack top - 1) cow. So we accumulate this value to answer (ans += 0), pop cow 1 (height of 3) until an empty stack or the stack top cow is taller than 7, and push cow 2 (height of 7). After that,

[0        ans += (i - stack.top() - 1), stack.pop()
[0 2
[0 2 3

When we meet cow 4 (height of 12), another cow that higher than the stack top cow 3 (height of 4). Cow 3 then can see 0 cow, cow 2 (height of 7) can see 1 cow, and cow 0 (height of 10) can see 3 cows. Let's break it up,

i = 4   # current cow index
top_idx = 3   # top index
c_3 = i - 3 - 1 = 0, then stack.pop(), ans += c_3, top_idx = 2
c_2 = i - 2 - 1 = 1, then stack.pop(), ans += c_2, top_idx = 0
c_0 = i - 0 - 1 = 3, then stack.pop(), ans += c_0, stack empty

Then push cow 4 and cow 5 (height of 12 and 2) into the stack,

[4
[4 5

When we reach the right-most cow, we push a cow that has infinite height, then we can calculate the number of cows that cow 4 and cow 5 can see.

i = 6
top_idx = 4
c_4 = i - 4 - 1, then stack.pop(), ans += c_4, top_idx = 5
c_5 = i - 5 - 1, then stack.pop(), ans += c_5, stack empty

Then push the infinite height cow into the stack (optional) as we return the final answer.

The code is shown in the following code block:

LeetCode 42 Trapping Rain Water

Another problem is LeetCode 42. You can try solving this problem yourself. The solution code is provided on GitHub Gist, so feel free to explore it.