City Connection Problem

Let us consider a scenario of connecting cities with highways. The question is how we can determine if it is possible to travel from one city to another only by highways. To solve this problem, we can use the Union-Find Disjoint Sets, also known as disjoint sets.

Reading in Roads Info

Since we are focusing on the interconnections between cities on the map, we will denote two interconnected cities as X –- Y, where X and Y represent the city names. For example:

1 -- 3
1 -- 2
2 -- 4
3 -- 4
5 -- 6
6 -- 7

The notations -- indicate a interconnection of each pair of cities. We can build a graph according to the specification, like this:

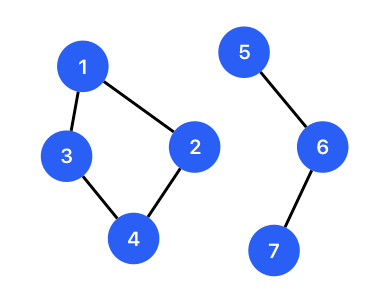
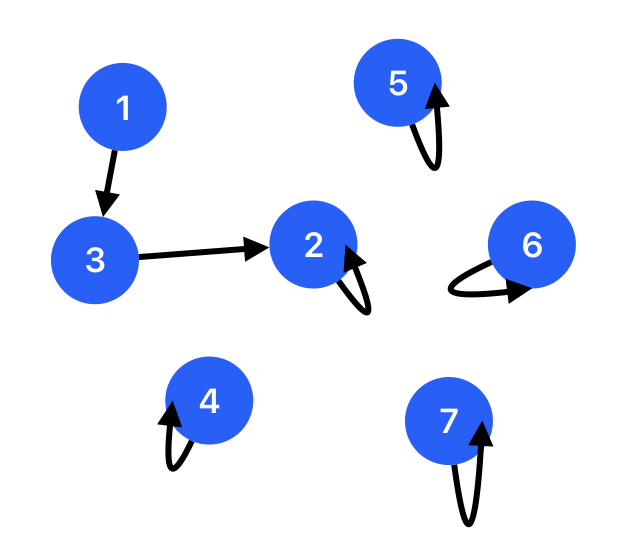
In this graph, if we want to check if city 4 is connected with city 7, we can use search algorithms such as Depth-first Search (DFS) or Breadth-first Search (BFS). If we want to make sure we cannot go to city 7 from city 4, we must traverse all around the left 1-2-4-3-1 trace. The time complexity of the checking is $O(N)$.

If we are focusing on the knowledge about if they are interconnected, the more time-efficient way is to build disjoint sets, then we can lower down the time complexity with the help of trees.

How Disjoint Set works

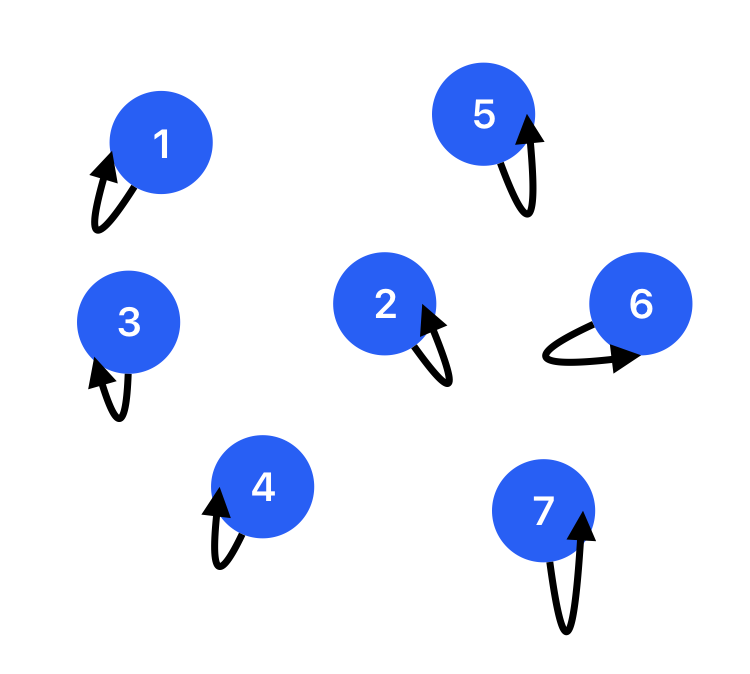
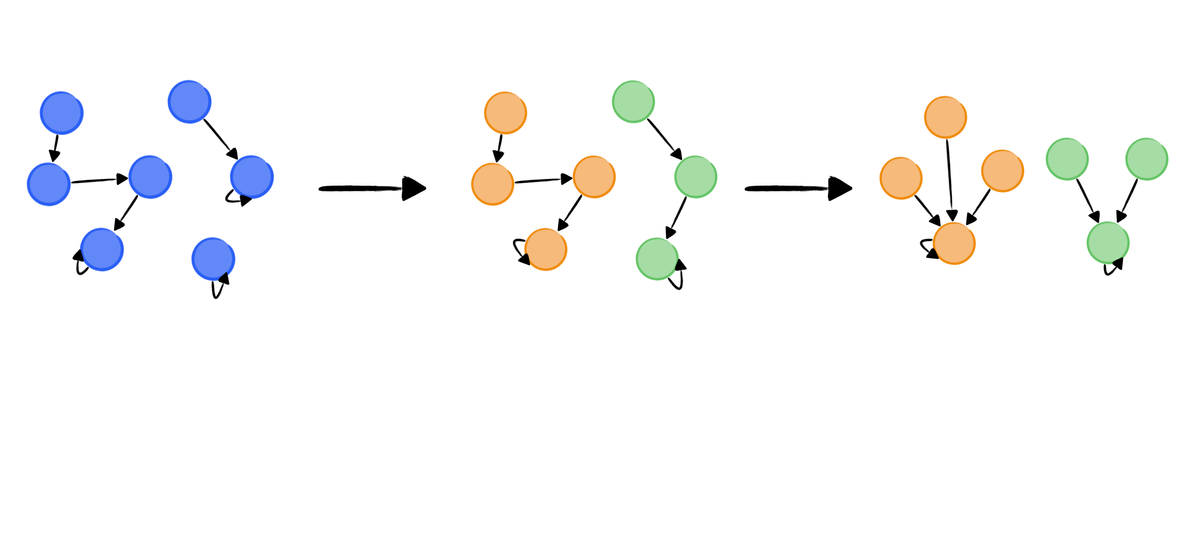
Modeling this problem using the graph theory, we can regard each cities as a node, as shown in the figure. At first, we can initiate each node having their parent node as itself since disjoint sets work as a forest (trees) data structure (tree have a root node). In the current scenario, every node is a root node and there are 7 trees in this figure, which can easily illustrated by the Python code:

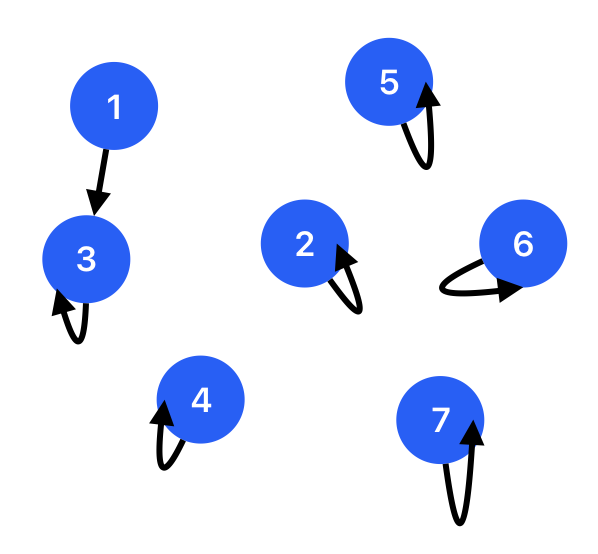
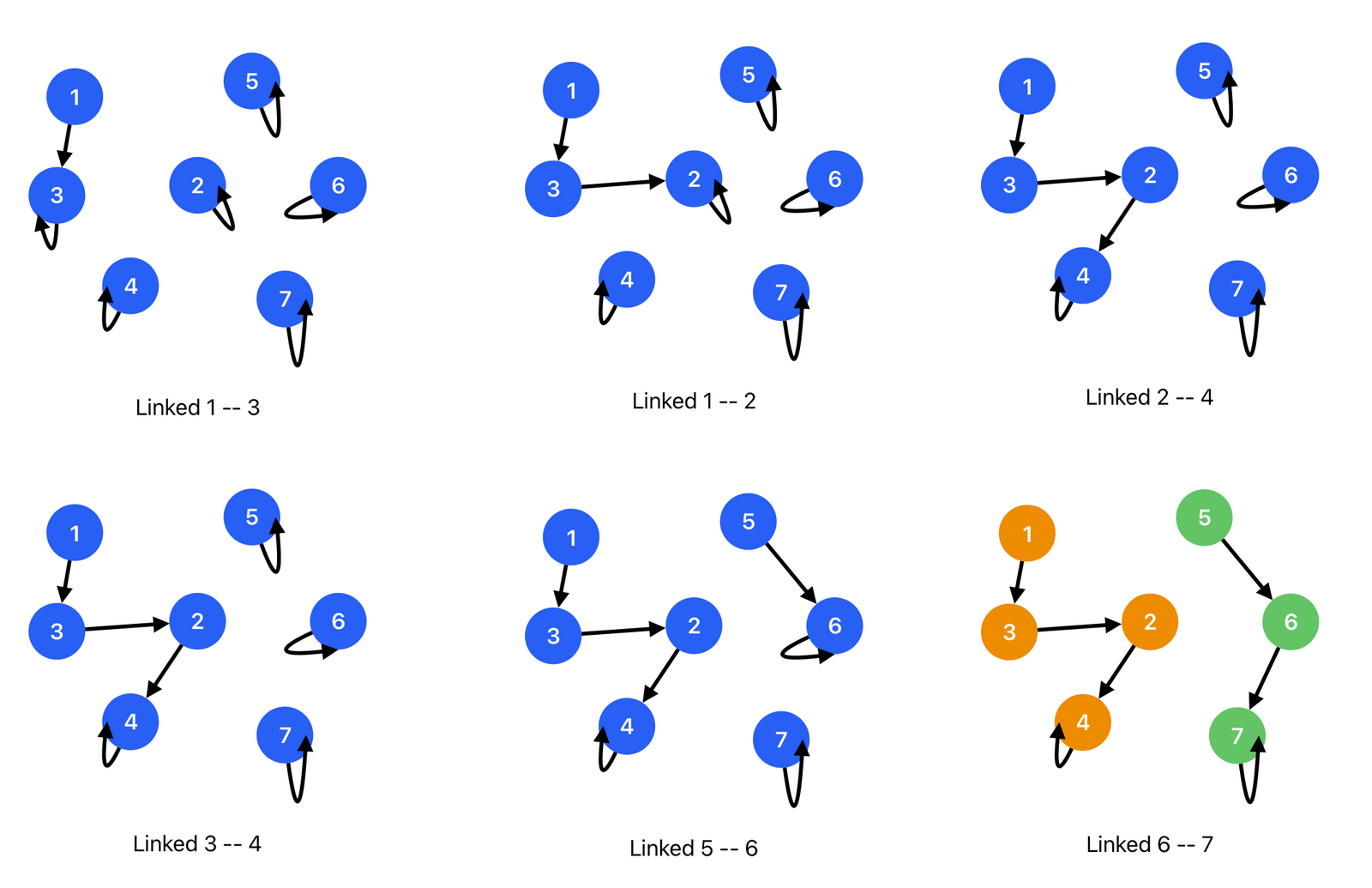
Now we read in the data of how the junctions connected. Such as 1 -- 3, we need to change the parent of one node to another (whatever it is node 1 or node 3). The diagram illustrate the result of disjoint sets after alternation.

Okay, seems easy. Let us do the next link, 1 -- 2. Follow with the rules of tree, a node in a tree can only have one parent. If we change the parent of node 1 to node 2, node 3 could no longer be parent of node 1, which causes loss of information. The solution is pretty straight-forward, since each root node have parent node as themselves. Since each group of interconnected nodes can be identified by different root nodes, if node 2 want to join the group which having root node is node 3, then just simply change the parent of node 3 (group root node) to node 2.

Here are the rules:

1. If we are going to link two nodes which are in different groups (single node is also considered as a group), link the root nodes of each groups together.

2. If we are going to link two nodes which are in the same group (having the same group root node), do nothing.

The Python code for finding a group's root node is:

By applying the rule, we can finally get following trees after linked 6 -- 7:

In the final result, 6 -- 7, we have two groups, root node 4 and root node 7. Back to the question, to check if node 4 and node 7 are interconnected, we need to check if parent_of(4) is equal to parent_of(7).

However, currently, the worse case of disjoint sets is that trees are builded as a linked list (degenerate into a chain), as the example given. The time complexity is still similar to that of utilizing search algorithms. To tackle the issue, we must update the current disjoint set into a 1-depth tree, as illustrated in the following figure.

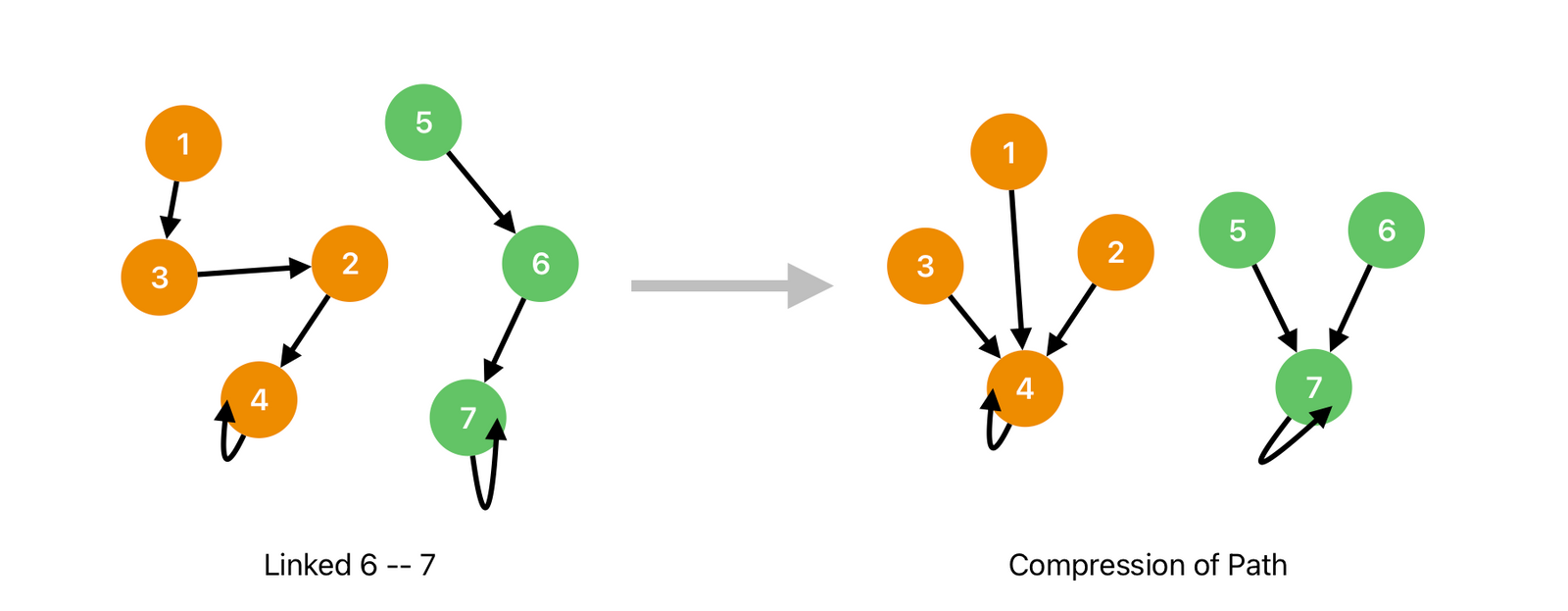
The following updated parent_of(node) function can implement this action

When we utilize path compression to obtain disjoint sets, the time complexity of checking if two nodes are interconnected becomes optimized to the level of the tree, which is $O(\alpha(n))$.

The average time complexity for each operation in a disjoint-set data structure is only $O(\alpha(n))$, where $\alpha$ is the inverse of the Ackermann function. The growth of $\alpha(n)$ is extremely slow, meaning that the average running time for a single operation can be considered a very small constant ^[1].

The definition of the Ackermann function $A(m, n)$ is:

$$
A(m, n) =
\begin{cases}
n+1&\text{if }m=0 \\
A(m-1,1)&\text{if }m>0\text{ and }n=0 \\
A(m-1,A(m,n-1))&\text{otherwise}
\end{cases}
$$