Problem Intro

The eight queens problem is based on Chess, it's for determining how to place 8 queens on a chessboard of size 8 × 8, and make sure any of the queens cannot capture the other 7 queens. To get this approach, any of two queens cannot be at the same row, column, and the same diagonal. Actually, it has been generalized into N queens problem which the board size is N × N and the number of queens is also N, this N queens problem is solvable iff N = 1 or N ≥ 4.

Implementing Algorithms

Depth-First Search (DFS)

Depth-First Search (abbr. DFS) Algorithms is famous algorithms for traversal Searching-Tree and Graph. The way of traversal is Depth-First which steps into sub-nodes rather than siblings nodes, and backtracking (goes back to its super-node) when all the edges of the current node have been visited. And ending the searching when all of the nodes have been visited. DFS is a famous algorithm in Graph Theory, it can be used to determine graph-related topological sorting tables, which can make problem-solving such as shortest-path more straightforward.

Here is an example of using DFS to traversal a tree, you can follow the path to emulate the DFS process.

def traversalTree(root):
  root.visited = True                    # Marking Visited
  if root.hasSub():
    for node in root.sub:
        traversalTree(node)              # Recursion
  else:
    return                               # Backtracking

# DFS Order  
1 ➔ 2 ➔ 3 ➔ 4 ➔ 5 ➔ 6 ➔ 7 ➔ 8 ➔ 9 ➔ 10 ➔ 11 ➔ 12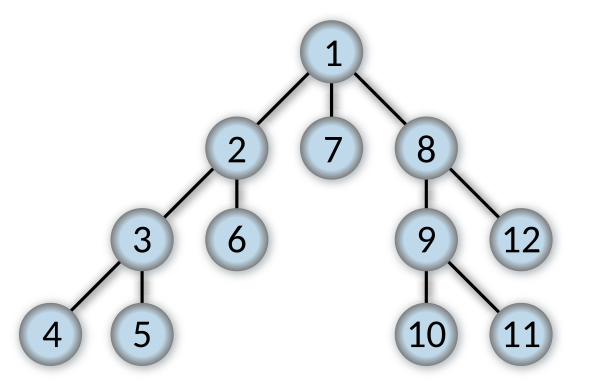

Implementation of such kinds of problems is recursion and backtracking. Note that the following example is a general solution of recursion and backtracking which are the keys of DFS.

/* DFS template implemented in C++
** Using C/C++ to solve N-Queen problem is by far the fastest approach
** So I will use C++ in following codes
*/
void dfs(int now) {
    // ...
    for (int j = 1; j <= N; j++) {
        if ((!d[j]) && (!l[now + j]) && (!r[now - j + N])) {
            pos[now] = j; d[j] = 1; l[now + j] = 1; r[now - j + N] = 1; // Marking
            dfs(now + 1); // Recursion
            d[j] = 0; l[now + j] = 0; r[now - j + N] = 0; // Backtracking
        }
        // ...
    }

Queens Placement Method

We need spaces to save queens' positions, in this problem, it's obvious that any of two queens cannot be in the same row or same column. Placing queens from top to bottom, and recording in a specific row in which grid cannot be placed with a queen, which needs dynamic arrays to maintain. pos[N] array to record every column's queen position(in which row), pos[2] = 3 means there is a queen in row 3 column 2. d[N] is for maintaining every queens' down-side cannot have another queen. l[N] and r[N] arrays are for maintaining left-bottom and right-bottom grids cannot have queens. when every recursion to deeper, l and r arrays to be calculated whether the position can place a queen. This process is very easy to understand using the coordinate system.

C++ Code

/* N-Queens Problem
** Code by Ex10si0n
*/

#include <iostream>
#include <cstdio>
#include <cstdlib>

using namespace std;
int N, cnt, pos[100], d[100], r[100], l[100];

void print() {
    if (cnt > 3)
        return;
    for (int i = 1; i <= N; i++)
        cout << pos[i] << " ";
    cout << endl;
}

void dfs(int now) {
    if (now > N) {
        cnt++;
        print();
        return;
    }
    else {
        for (int j = 1; j <= N; j++) {
            if ((!d[j]) && (!l[now + j]) && (!r[now - j + N])) {
                pos[now] = j; d[j] = 1; l[now + j] = 1; r[now - j + N] = 1;
                dfs(now + 1);
                d[j] = 0; l[now + j] = 0; r[now - j + N] = 0;
            }
        }
    }
}

int main() {
    cin >> N;
    dfs(1);
    cout << cnt << endl;
    return 0;
}

/*

   1 2 3 4 (x)
 1 . x . .
 2 l d r . 
 3 . d . r
 4 . d . .
(y)

x ➜ d, l, r;
d.all = x;
r.all = x - y;
l.all = x + y;

. . . x . .
x . . . . .
. . . . x .
. x . . . .
. . . . . x
. . x . . .

*/

Bonus: Implemented by C++ bit Operations

int upperlim = (1 << n) - 1; // Initialize upperlim with all 1 digits
void work(int row, int ld, int rd) {
    int pos, p;
    if (row != upperlim) {
        pos = upperlim & ~(row | ld | rd);
        // row | ld | rd represent next permutation not be recorded by 1，and negate this value，that is marking avaliable by 1，OR with upperlim，result is the next recording position
        while (pos != 0) {
            p = pos & -pos; // Marked by the rightest 1
            pos = pos - p; // Marking pos
            work(row | p, (ld | p) << 1, (rd | p) >> 1); // search next permutation
        }
    }
    else
        sum++;
}